Scale of twelve notes of mixed whole and half steps/notes.
Ramsay
she is found to have produced the Chromatic scale of twelve semitones, derived from her own vital operations; so that there are no anomalies. It is a degradation of the mathematical primes to apply them to the getting of the semitones of the chromatic scale, as even Euler himself mistakenly does. The mathematical ratios lead the way in getting the notes of the diatonic scale, and that is all that is required of them. The true praise to the ratios is that they have constituted an organic structure with form and life-powers adapted for self-development. It would be little credit to the mother if the child required to be all its life-long pinned to her apron-strings. As the bird when developed so far leaves the shell, and is afterwards fully developed in new conditions; so the System of music when developed so far leaves the law of ratios, its mathematical shell, and is afterwards fully developed by other laws. Music has an inspirational as well as a mathematical basis, and when mathematicians do not recognize this they reckon without their host. [Scientific Basis and Build of Music, page 35]
Mathematicians have not recognized the life-power of the notes, and so they have misapplied their calculations, though these were perfect in themselves. Assuming the place of dictators, they say with an air of authority that, "strictly speaking, nothing could be more scientifically and musically untrue than the chromatic scale of twelve equal semitones as played on a tempered instrument; for in it, as in the diatonic scale, the same natural law prevails that no two tones of equal mathematical relations can melodically succeed each other." Saying that the same natural law prevails implies that they are reasoning from analogy; but in this assumption they are dictating to Nature. In a similar way they might assume that the interval of the octave, like the other intervals, should have a grave harmonic.2 But the fact that the octave interval has not a [Scientific Basis and Build of Music, page 36]
This subtracting and adding process of Nature by which she so freely handles the notes is the way she gives us the materials of the Chromatic Scale, in which an entirely new series of chords with strikingly different effects, and with exceedingly interesting, subtle, and at the same time easy progressions, is put in possession of the practical musician. This new series of chords forms, in fact, materials for the Chromatic System, which D. C. Ramsay has discovered, and which he has elaborated, as his custom was, exhaustively - his last labor in the interests of music science and art. [Scientific Basis and Build of Music, page 48]
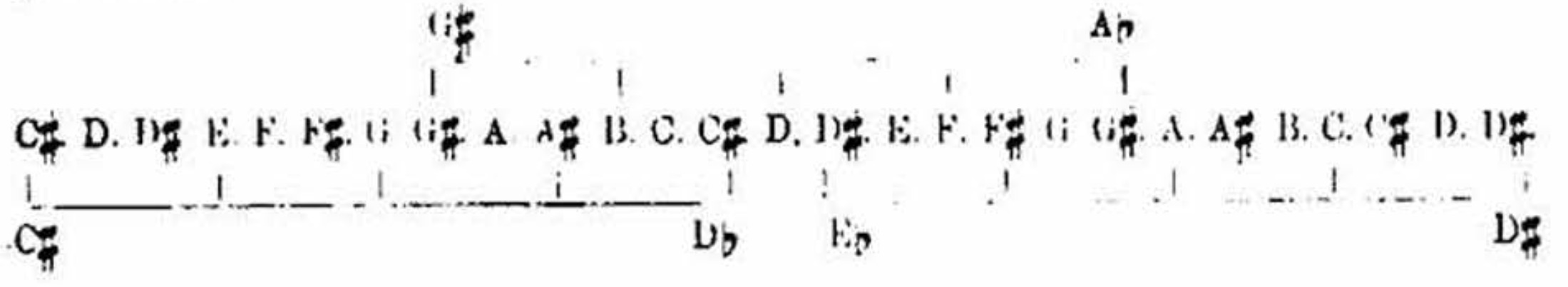
In the above line it will be readily observed that these three chromatic chords, having each of their intervals a minor third, involve, as necessary elements of their build, every one of the twelve semitones at one point or another of the line. This is a second witness to the legitimacy of the chromatic scale of twelve semitones. We have our first witness to the same in the evolution of the semitones progressively in the course of the modulations by which, in growth-like continuity, Nature links the successive keys; whether developed upward, as is the natural way of the majors; or downward, as in the natural way of the minors; or half upward and half downward, which is an expedient in order to simplify the signatures. In whichever direction the modulation is effected, one note is always divided, and must, true to Nature, be signified by placing a sharp or a ?, as the case may be, to the 4-comma altered interval, and this always leaves a 5-comma interval to occupy the place to which Nature has assigned such interval in the original scale. When this operation has been twelve times performed, we have the chromatic scale of twelve semitones. Thus by two witnesses the thing is established. By further examination of these chromatic chords we find other interesting features beside their witness to the twelve semitones of the octave. [Scientific Basis and Build of Music, page 56]
The Chromatic Scale is naturally the last to come into view, for it is not generated by a mathematical process at all. Chromatic intervals are indeed found in the scale as mathematically generated. The semitones between B-C and E-F are two chromatic intervals, and the chord which occurs between the major and the minor in the chord-scale when it begins with the minor mode is a chromatic chord, though in an uncompleted condition. But the making of the octave into a chromatic scale of twelve small or semi-tones, is the work of modulation from one key to another through the whole twelve keys in either the major or minor sphere; and this process is fully set forth in the pre-note to the chromatic treatise. [Scientific Basis and Build of Music, page 69]
The number of Chromatic Chords. Three chromatic chords exhaust the semitonic 12-foldness of the octave. The chromatic scale is a much more even thing than the diatonic; contrast is not its feature, and we may expect [Scientific Basis and Build of Music, page 72]
One purpose of this plate is to show that twelve times the interval of a fifth divides the octave into twelve semitones; and each of these twelve notes is the first note of a major and a minor scale. When the same note has two names, the one has sharps and the other has flats. The number of sharps and flats taken together is always twelve. In this plate will also be observed an exhibition of the omnipresence of the chromatic chords among the twice twelve scales. The staff in the center of the plate is also used as to show the whole 24 scales. Going from the major end, the winding line, advancing by fifths, goes through all the twelve keys notes; but in order to keep all within the staff, a double expedient is resorted to. Instead of starting from C0, the line starts from the subdominant F0, that is, one key lower, and then following the line we have C1, G2, etc., B6 proceeds to G? instead of F#, but the signature-number continues still to indicate as if the keys went on in sharps up to F12, where the winding line ends. Going from the minor end, the line starts from E0 instead of A0 - that is, it starts from the dominant of A0, or one key in advance. Then following the line we have B1, F#2, etc. When we come to D#5, we proceed to B? instead of A#6, but the signature-number continues as if still in sharps up [Scientific Basis and Build of Music, page 114]
This plate, in the outer stave, has the 32 notes which arise with mathematical development of twelve scales in advancing fifths. The notes are marked with sharps, flats, and commas. The flats and commas of lowering are placed on the left of the notes, in the order in which they arise, reading them from the note downward; the sharps and commas of rising on the right, also reading from the note upward. The whole of these 32 notes are brought within the compass of an octave. [Scientific Basis and Build of Music, page 119]
The inner stave contains the chromatic scale of twelve notes as played on keyed instruments. The flat and sharp phase of the intermediate notes are both given to indicate their relation to each other; the sharpened note being always the higher one, although seemingly on the stave the lower one. The two notes are the apotome minor apart overlapping each other by so much; ?D is the apotome lower than C#; ?E the apotome lower than D#; F# the apotome higher than ?G; G# the apotome higher than ?A; and A# the apotome higher than ?B. The figures for the chromatic scale are only given for the notes and their sharps; but in the mathematical series of notes the numbers are all given. [Scientific Basis and Build of Music, page 120]
Hughes
Here we see why music, as a science, takes the priority of painting; for if music is good, it is perfected by natural laws which cause its tones to melt into each other in the most delicate gradations, while the painter who endeavours to represent the exquisite variations of tints and lights in the living landscape is dependent entirely upon his own resources. The early writers on music were philosophers and mathematicians on the broad basis of general science, not on that of music only. Mathematicians, for the most part, have only studied the subject of musical sounds up to a certain point, and have then left it. The musician must take the chromatic scale—not as it exists in Nature, for that offered by the mathematician, without the ordinary compensations of conventional theory, is of no use to the practical musician. [Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies2, page 16]
the artificial system must not be mixed up. The wonders of Nature's laws in the developments of harmonies, consist in the beautiful adaption of keyed and all other musical instruments to a range commensurate with human powers. The chromatic scale of twelve notes (the thirteenth being the octave) is not the scale of Nature. To construct a musical instrument upon real divisions of musical tones, each of them being in correct ratio with the others, it would be necessary to have a larger number of tones to the octave. In the development of harmonies on the natural system, we trace the perfect adaptation of means to ends, meeting the intricacies of every musical instrument, including that most perfect of all— the human voice. [Harmonies of Tones and Colours, The Method of Development or Creation of Harmonies3, page 17]
See Also
Chromatic
major scale
minor scale
Musical Scale
natural scale
Ramsay - The Shifting Key with its unaltered form
Scale
Tempered scale
